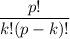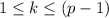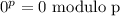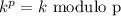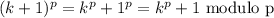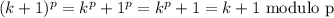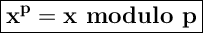Mathematics, 27.08.2020 22:01 kaylastronaut
Let p be a prime number. The following exercises lead to a proof of Fermat's Little Theorem, which we prove by another method in the next chapter. a) For any integer k with 0 ≤ k ≤ p, let (p k) = p!/k!(p - k)! denote the binomial coefficient. Prove that (p k) 0 mod p if 1 ≤ k ≤ p - 1. b) Prove that for all integers x, y, (x + y)^p x^? + y^p mod p. c) Prove that for all integers x, x^p x mod p.

Answers: 2


Another question on Mathematics

Mathematics, 21.06.2019 14:00
You purchased 8 pounds 10 ounces of candy from a candy shop. you want to split it equally among 3 classrooms at a local school.
Answers: 1

Mathematics, 21.06.2019 14:30
Find all the values of x that make 0.1x + 0.25(102 - x) < 17.10 true.
Answers: 1

Mathematics, 21.06.2019 21:30
A.s.a.! similarity in right triangles, refer to the figure to complete this proportionc/a = a/? a.) cb.) hc.) rd.) s
Answers: 1

Mathematics, 21.06.2019 23:10
The input to the function is x and the output is y. write the function such that x can be a vector (use element-by-element operations). a) use the function to calculate y(-1.5) and y(5). b) use the function to make a plot of the function y(x) for -2 ≤ x ≤ 6.
Answers: 1
You know the right answer?
Let p be a prime number. The following exercises lead to a proof of Fermat's Little Theorem, which w...
Questions















History, 04.04.2020 10:54