Mathematics, 19.05.2020 22:15 crystalrc3414

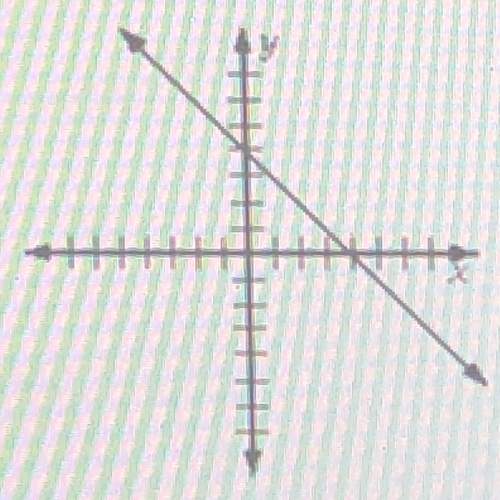
Let a(x)=3x^3+1a(x)=3x 3 +1a, left parenthesis, x, right parenthesis, equals, 3, x, cubed, plus, 1, and b(x)=x^2b(x)=x 2 b, left parenthesis, x, right parenthesis, equals, x, squared. When dividing aaa by bbb, we can find the unique quotient polynomial qqq and remainder polynomial rrr that satisfy the following equation: \dfrac{a(x)}{b(x)}=q(x) + \dfrac{r(x)}{b(x)} b(x) a(x) =q(x)+ b(x) r(x) start fraction, a, left parenthesis, x, right parenthesis, divided by, b, left parenthesis, x, right parenthesis, end fraction, equals, q, left parenthesis, x, right parenthesis, plus, start fraction, r, left parenthesis, x, right parenthesis, divided by, b, left parenthesis, x, right parenthesis, end fraction, where the degree of r(x)r(x)r, left parenthesis, x, right parenthesis is less than the degree of b(x)b(x)b, left parenthesis, x, right parenthesis. What is the quotient, q(x)q(x)q, left parenthesis, x, right parenthesis? q(x)=q(x)=q, left parenthesis, x, right parenthesis, equals What is the remainder, r(x)r(x)r, left parenthesis, x, right parenthesis? r(x)=r(x)=r, left parenthesis, x, right parenthesis, equals

Answers: 1

Show answers

Another question on Mathematics

Mathematics, 21.06.2019 17:40

Find the volume of the described solid.the solid lies between planes perpendicular to the x-axis at x = 0 and x=7. the cross sectionsperpendicular to the x-axis between these planes are squares whose bases run from the parabolay=-31x to the parabola y = 30/x.a) 441b) 147c) 864d) 882

Answers: 1

Answer

Mathematics, 21.06.2019 21:00

Can some one explain how to slove specifically, what is the value of x? 0.9(x+1.4)-2.3+0.1x=1.6 enter the answer as a decimal in the box. x= ?

Answers: 2

Answer

Mathematics, 21.06.2019 22:40

What are the excluded values? m+5/mn+3m

Answers: 1

Answer

Mathematics, 22.06.2019 01:40

Suppose we have a set of small wooden blocks showing the 26 letters of the english alphabet, one letter per block. (think of scrabble tiles.) our set includes 10 copies of each letter. we place them into a bag and draw out one block at a time. (a) if we line up the letters on a rack as we draw them, how different ways coukl we fill a rack of 5 letters? (b) now suppose we just toss our chosen blocks into a pile, and whenever we draw a letter we already have, we put it back in the bag and draw again. how many different piles of 5 blocks could result? possible? piles will contain at least one repeated letter? (c) if we draw out 5 blocks wit hout looking at them, how many different piles are (d) if we draw out 5 blocks without looking at them, how many of the possible 2. (4) consider the following formula. 12 give two different proofs, one using the factorial formulas and the other combina torial.

Answers: 3

Answer

You know the right answer?

Let a(x)=3x^3+1a(x)=3x 3 +1a, left parenthesis, x, right parenthesis, equals, 3, x, cubed, plus, 1,...

Questions