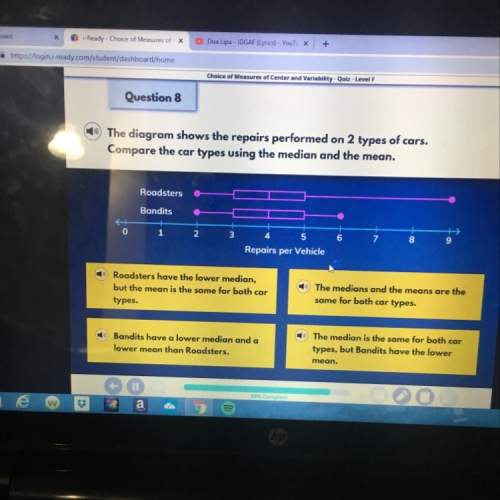
Mathematics, 22.06.2021 21:50 yqui8767
David found and factored out the GCF of the polynomial 80b4 – 32b2c3 + 48b4c. His work is below.
GFC of 80, 32, and 48: 16
GCF of b4, b2, and b4: b2
GCF of c3 and c: c
GCF of the polynomial: 16b2c
Rewrite as a product of the GCF:
16b2c(5b2) – 16b2c(2c2) + 16b2c(3b2)
Factor out GCF: 16b2c(5b2 – 2c2 + 3b2)
Which statements are true about David’s work? Check all that apply.
The GCF of the coefficients is correct.
The GCF of the variable b should be b4 instead of b2.
The variable c is not common to all terms, so a power of c should not have been factored out.
The expression in step 5 is equivalent to the given polynomial.
In step 6, David applied the distributive property.

Answers: 1


Another question on Mathematics

Mathematics, 21.06.2019 16:00
Mr and mrs smith buy tickets for themselves and their four children. the cost of an adult ticket is ? 6 more than the adult ticket. the total cost of the six tickets is ? 40.50 work out the cost of an adult ticket. in your working let c be the cost of the child ticket and a be the cost of the adult ticket.
Answers: 1


Mathematics, 21.06.2019 22:30
Find the area of the region that is inside r=3cos(theta) and outside r=2-cos(theta). sketch the curves.
Answers: 3

Mathematics, 21.06.2019 23:30
Answer each of the questions for the following diagram: 1. what type of angles are these? 2. solve for x. what does x equal? 3. what is the measure of the angles?
Answers: 1
You know the right answer?
David found and factored out the GCF of the polynomial 80b4 – 32b2c3 + 48b4c. His work is below.
GF...
Questions










Mathematics, 24.05.2021 14:00




Mathematics, 24.05.2021 14:00