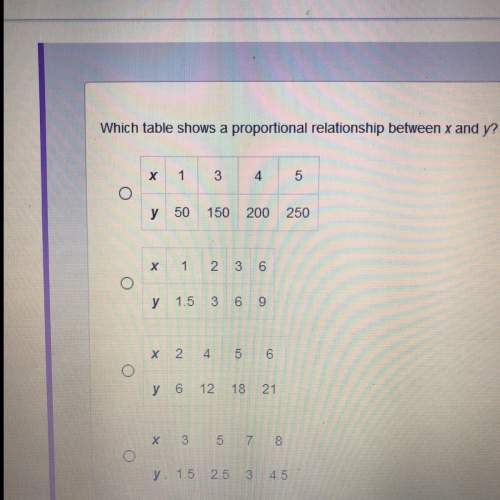
Mathematics, 05.02.2020 10:02 lashaydews12
Aseafood company produces cans of tuna. each can gets wrapped with a paper label. if every can has a radius of 8.3 centimeters, what is the approximate length of the paper required to cover two cans?
26.062 centimeters
52.124 centimeters
104.248 centimeters
216.3146 centimeters

Answers: 1


Another question on Mathematics

Mathematics, 21.06.2019 14:40
The class wants to raise a total of $750.if they receive a profit of $1.25 from each candybar sold, how many bars must they sell to reachtheir goal
Answers: 1

Mathematics, 22.06.2019 00:00
The average length of a king cobra is 3.7 m. the record length is 1.88 m longer than the average. how long is the record holder?
Answers: 1

Mathematics, 22.06.2019 06:00
1. which answer is the solution set to the given inequality? 2x+6< 8 a. x e (-∞,1) b. x e [1,∞) c. x e (1,∞) d. x e (-∞,1] 2. which answer represents the given compound inequality in interval notation? x≥12 or x< -4 a. x e [-4, 12) b. x e (-∞, -4) u [12,∞) c. x e (-∞, -4] u (12,∞) d. x e (-4,12] 3. which answer is the solution set of the given compound inequality? 7> x+6 or x-2≥3 a. x e (-∞, 1) u [5,∞) b. x e (1, 5] c. x e (-∞, 1) ∩ [5,∞) d. x e [1,5) 4. which conjunction or disconjunction is equivalent to the given absolute value inequality? |x+3|> 12 a. x+3> 12 and x+3< -12 b. x+3< 12 and x+3> -12 c. x+3< 12 or x+3> -12 d. x+3> 12 or x+3< -12
Answers: 1

Mathematics, 22.06.2019 07:30
Ece 202: problem set 1 due: june 14, 2019 (friday) the first 3 questions of this homework assignment covers some fundamental mathematical concepts that will play a role in this course. the remaining questions are on basic signals and laplace transforms. 1. a review of complex numbers. (a) compute the magnitude and the phase of the complex numbers −4 +j, and write them in polar form (i.e., of the form rejθ). also, plot the complex number in the complex plane. (b) simplify the complex number 1 4 − √ 1 2 − j √ 2 22 and write them in cartesian form. (c) consider the complex number s = z1z2 · · ·zm p1p2 · · · pn , where each zi is a complex number with magnitude |zi | and phase ∠zi , and each pi is a complex number with magnitude |pi | and phase ∠pi . write the magnitude and phase of s in terms of the magnitudes and phases of z1, z2, . . , zm, p1, p2, . . , pn. 2. a review of differentiation. (a) find df dx for the following functions. i. f(x) = (1−4x) 2 √ x . ii. f(x) = √ 1 + tan x. (b) find dy dx for the equation e x sin y + cos2 x cos y − x 3 = 0.
Answers: 1
You know the right answer?
Aseafood company produces cans of tuna. each can gets wrapped with a paper label. if every can has a...
Questions


Spanish, 03.01.2020 12:31





Mathematics, 03.01.2020 12:31

Mathematics, 03.01.2020 12:31

English, 03.01.2020 12:31


Biology, 03.01.2020 12:31

History, 03.01.2020 12:31



History, 03.01.2020 12:31

History, 03.01.2020 12:31




History, 03.01.2020 12:31