
Mathematics, 27.03.2021 06:00 kallee10
A manufacturing company produces 3 different products A, B, and C. Three types of components, i. e., X, Y, and Z, are used in the production of these products. One unit of product A requires 2 units of X, 2 units of Y, and 2 units of Z. One unit of product B requires 1 unit of X, 3 units of Y, and 2 units of Z. One unit of product C requires 1 unit of X, 2 units of Y, and 3 units of Z. Currently, the company has no existing inventory of the components. The company can purchase X at the price of $20 per unit but no more than 300 units due to the supplier's limited capacity constraint. The company can purchase Y at the price of $30 per unit without any upper limit. The company can purchase Z at the full price of $25 per unit for the first 100 units but the per unit price drops to $20 for the remaining units if any i. e., the purchase quantity in excess of 100 units). The market prices of the three products are $200 for A, $240 for B and $220 for C. The company knows that the demand for products A, B, and Care equal to 100, 80, and 90 units, respectively. Therefore, the company should not produce more than the demand for each product. However, the company incurs a per unit penalty of $40 for any unsatisfied demand. The company needs to decide the component płarchase plan and the production mix decisions to maximize its profits subject to all the business constraints described above. Formulate the company's problem as an optimization problem, i. e., providing the mathematical expressions for the decision variables, the objective function, and the constraints.

Answers: 3


Another question on Mathematics

Mathematics, 21.06.2019 14:30
The number of revolutions of two pulleys is inversely proportional to their diameters. if a 24-inch diameter pulley making 400 revolutions per minute is belted to an 8-inch diameter pulley, find the number of revolutions per minute of the smaller pulley.
Answers: 1

Mathematics, 21.06.2019 15:00
Which statement is always true? a. square bcdf is a rectangle. b. rectangle gjkm is a square. c. quadrilateral stpr is a trapezoid. d. parallelogram abcd is a rhombus.
Answers: 2

Mathematics, 21.06.2019 22:10
Asix-sided number cube is rolled twice. what is the probability that the first roll is an even numbe and the second roll is a number greater than 4?
Answers: 1

Mathematics, 21.06.2019 23:00
Ithink i know it but i want to be sure so can you me out ?
Answers: 1
You know the right answer?
A manufacturing company produces 3 different products A, B, and C. Three types of components, i. e.,...
Questions


Social Studies, 18.12.2021 04:00



Mathematics, 18.12.2021 04:00

History, 18.12.2021 04:00




Computers and Technology, 18.12.2021 04:00




Social Studies, 18.12.2021 04:00


Biology, 18.12.2021 04:00

Mathematics, 18.12.2021 04:00



Computers and Technology, 18.12.2021 04:00

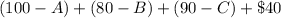
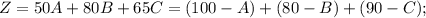
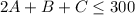 due to 2A, B, C units of X are used in manufacturing A, B, C units of products A, B, C respectively.
due to 2A, B, C units of X are used in manufacturing A, B, C units of products A, B, C respectively.

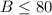
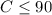
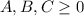 because they are positive quantities
because they are positive quantities
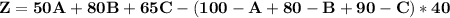
 Decision Varaibles;
Decision Varaibles;



