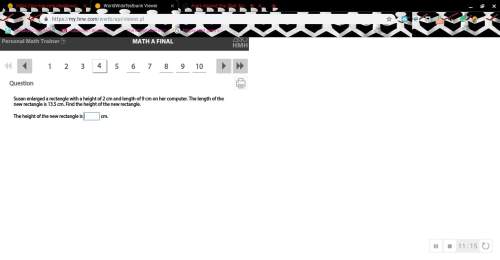
Mathematics, 04.03.2021 04:30 gudtavosanchez19
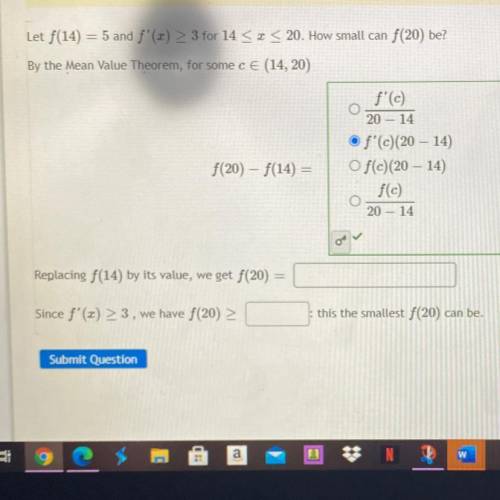
Let f(14) = 5 and f'(2) > 3 for 14 < I< 20. How small can f(20) be?
By the Mean Value Theorem, for some c E (14, 20)
f'(c)
20 - 14
of'(c)(20 - 14)
Of(c)(20 - 14)
f(c)
20 - 14
F(20) - f(14) =
Replacing f(14) by its value, we get f(20)
Since f'(2) >3, we have f(20) >
this the smallest f(20) can be.

Answers: 3


Another question on Mathematics


Mathematics, 21.06.2019 20:00
Given the equation y − 4 = three fourths(x + 8) in point-slope form, identify the equation of the same line in standard form. −three fourthsx + y = 10 3x − 4y = −40 y = three fourthsx + 12 y = three fourthsx + 10
Answers: 1


Mathematics, 22.06.2019 00:50
Assume that adults have iq scores that are normally distributed with a mean of mu equals 100 and a standard deviation sigma equals 20. find the probability that a randomly selected adult has an iq between 80 and 120.assume that adults have iq scores that are normally distributed with a mean of mu equals 100 and a standard deviation sigma equals 20. find the probability that a randomly selected adult has an iq between 80 and 120.
Answers: 3
You know the right answer?
Let f(14) = 5 and f'(2) > 3 for 14 < I< 20. How small can f(20) be?
By the Mean Value Theo...
Questions


Mathematics, 13.09.2019 22:10


Chemistry, 13.09.2019 22:10

Spanish, 13.09.2019 22:10

Mathematics, 13.09.2019 22:10






Mathematics, 13.09.2019 22:20





Mathematics, 13.09.2019 22:20



English, 13.09.2019 22:20