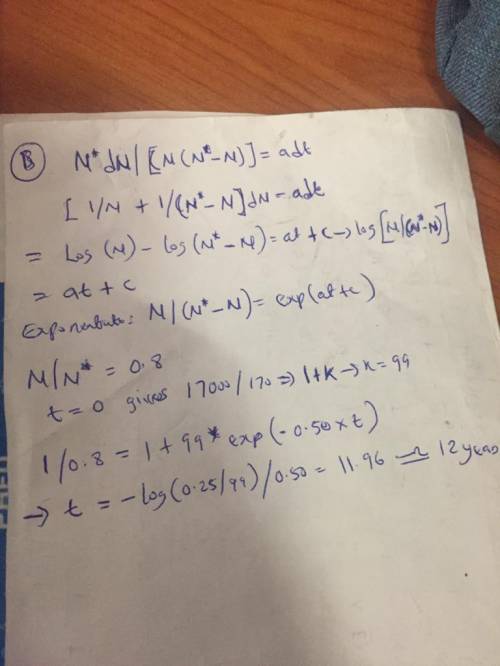Mathematics, 01.02.2021 21:00 cefindley14
Let N* be the total number of ranchers in Uruguay, and N(t) be the number of ranchers who have adopted an improved pasture technology there. Assume that the rate of adoption, , is proportional to both the number who have adopted the technology and the fraction of the ranchers who have not (and so are susceptible to conversion). Let a be the proportionality constant.
a. Write down the differential equation modeling N(t).
b. According to Banks (1993), N* = 17000, N(0) = 170, a = 0.5 per year.
Determine how long it takes for the improved pasture technology to spread to 80% of the population of the ranchers.

Answers: 2


Another question on Mathematics


Mathematics, 21.06.2019 18:00
Since opening night, attendance at play a has increased steadily, while attendance at play b first rose and then fell. equations modeling the daily attendance y at each play are shown below, where x is the number of days since opening night. on what day(s) was the attendance the same at both plays? what was the attendance? play a: y = 8x + 191 play b: y = -x^2 + 26x + 126
Answers: 1

Mathematics, 21.06.2019 21:40
Which statement is true about a number and its additive inverse? a. their product is always one. b. their sum is always one. c. they are always reciprocals of each other. d. their sum is always zero.
Answers: 1

Mathematics, 21.06.2019 22:00
Rewrite so the subject can be y in the formula d=m-y/y+n
Answers: 1
You know the right answer?
Let N* be the total number of ranchers in Uruguay, and N(t) be the number of ranchers who have adopt...
Questions

History, 07.04.2021 21:10


Mathematics, 07.04.2021 21:10

Biology, 07.04.2021 21:10

Biology, 07.04.2021 21:10


Mathematics, 07.04.2021 21:10

History, 07.04.2021 21:10


Mathematics, 07.04.2021 21:10

Mathematics, 07.04.2021 21:10


Social Studies, 07.04.2021 21:10




Mathematics, 07.04.2021 21:10



Social Studies, 07.04.2021 21:10