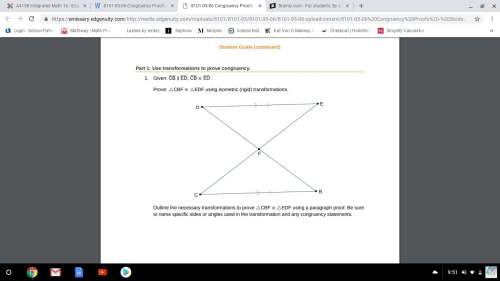
Mathematics, 25.01.2021 20:00 leannaadrian
Ivan used coordinate geometry to prove that quadrilateral EFGH is a square. Figure EFGH is shown. E is at negative 2, 3. F is at 1, 6. G is at 4, 3. H is at 1, 0. Statement
Reason 1. Quadrilateral EFGH is at E (−2, 3), F (1, 6), G (4, 3), and H (1, 0) 1. Given
2.__?__ 2.segment EF E (−2, 3) F (1, 6) d equals the square root of the quantity 1 plus 2 all squared plus 6 minus 3 all squared d equals the square root of the quantity 3 squared plus 3 squared equals the square root of 18 equals 3 times the square root of 2 segment FG F (1, 6) G (4, 3) d equals the square root of the quantity 4 minus 1 all squared plus 3 minus 6 all squared d equals the square root of the quantity 3 squared plus negative 3 squared equals the square root of 18 equals 3 times the square root of 2 segment GH G (4, 3) H (1, 0) d equals the square root of the quantity 1 minus 4 all squared plus 0 minus 3 all squared d equals the square root of the quantity negative 3 squared plus negative 3 squared equals the square root of 18 equals 3 times the square root of 2 segment EH E (−2, 3) H (1, 0) d equals the square root of the quantity 1 plus 2 all squared plus 0 minus 3 all squared d equals the square root of the quantity 3 squared plus negative 3 squared equals the square root of 18 equals 3 times the square root of 2
3. segment EF is parallel to segment GH 3. segment EF E (−2, 3) F (1, 6) m equals 6 minus 3 over 1 plus 2 equals 3 over 3 equals 1 segment GH G (4, 3) H (1, 0) m equals 0 minus 3 over 1 minus 4 equals negative 3 over negative 3 equals 1
4. __?__ 4. segment EH E(−2, 3) H (1, 0) m equals 0 minus 3 over 1 plus 2 equals negative 3 over 3 equals negative 1 segment FG F (1, 6) G (4, 3) m equals 3 minus 6 over 4 minus 1 equals negative 3 over 3 equals negative 1 5. segment EF and segment GH are perpendicular to segment FG
5. The slope of segment EF and segment GHis 1. The slope of segment FG is −1.
6. __?__ 6. The slope of segment FG and segment EH is −1. The slope of segment GH is 1. 7. Quadrilateral EFGH is a square 7. All sides are congruent, opposite sides are parallel, and adjacent sides are perpendicular.
Which of the following completes statement 4 of the proof?
A. segment EF, segment FG, segment GH, and segment EH are congruent
B. segment EF is parallel to segment GH
C. segment EH is parallel to segment FG
D. segment FGand segment EH are perpendicular to segment GH

Answers: 3


Another question on Mathematics

Mathematics, 20.06.2019 18:04
30 determine the coefficient on x 12 y 24 x12y24 in ( x 3 + 2 x y 2 + y + 3 ) 18 . (x3+2xy2+y+3)18. (be careful, as x x and y y now appear in multiple terms! )
Answers: 3

Mathematics, 21.06.2019 15:40
Given the following sampling distribution of one mean with a sample size 49, from a normally distributed population,find the population standard deviation, o.79828588912497
Answers: 3

Mathematics, 21.06.2019 17:10
The random variable x is the number of occurrences of an event over an interval of ten minutes. it can be assumed that the probability of an occurrence is the same in any two-time periods of an equal length. it is known that the mean number of occurrences in ten minutes is 5.3. the appropriate probability distribution for the random variable
Answers: 2

Mathematics, 21.06.2019 17:30
Write an expression that has three terms and simplifies to 4x - 7. identify the coefficient(s) and constant(s) in your expression
Answers: 1
You know the right answer?
Ivan used coordinate geometry to prove that quadrilateral EFGH is a square. Figure EFGH is shown. E...
Questions

Social Studies, 20.09.2019 16:00

English, 20.09.2019 16:00

Mathematics, 20.09.2019 16:00



History, 20.09.2019 16:00




Mathematics, 20.09.2019 16:00





Biology, 20.09.2019 16:00


History, 20.09.2019 16:00


Mathematics, 20.09.2019 16:00