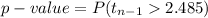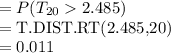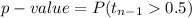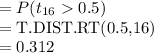Mathematics, 02.11.2020 17:00 alfonso55
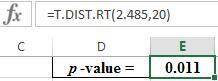
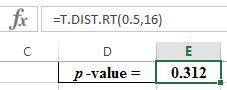
An independent random sample is selected from an approximately normal population with an unknown standard deviation. Find the p-value for the given set of hypotheses and T test statistic. (a) HA: μ > 0.5, n = 21, T = 2.485 p-value > 0.100 0.050 < p-value < 0.100 0.025 < p-value < 0.050 0.010 < p-value < 0.025 0.005 < p-value < 0.010 p-value < 0.005 Determine if the null hypothesis would be rejected at α = 0.01. reject H0 fail to reject H0 Changed: Your submitted answer was incorrect. Your current answer has not been submitted. (b) HA: μ < 3, n = 17, T = 0.5 p-value > 0.100 0.050 < p-value < 0.100 0.025 < p-value < 0.050 0.010 < p-value < 0.025 0.005 < p-value < 0.010 p-value < 0.005 Determine if the null hypothesis would be rejected at α = 0.01.

Answers: 2


Another question on Mathematics




Mathematics, 21.06.2019 20:50
An automobile assembly line operation has a scheduled mean completion time, μ, of 12 minutes. the standard deviation of completion times is 1.6 minutes. it is claimed that, under new management, the mean completion time has decreased. to test this claim, a random sample of 33 completion times under new management was taken. the sample had a mean of 11.2 minutes. assume that the population is normally distributed. can we support, at the 0.05 level of significance, the claim that the mean completion time has decreased under new management? assume that the standard deviation of completion times has not changed.
Answers: 3
You know the right answer?
An independent random sample is selected from an approximately normal population with an unknown sta...
Questions


Social Studies, 23.10.2020 14:00



Mathematics, 23.10.2020 14:00

Mathematics, 23.10.2020 14:00



Mathematics, 23.10.2020 14:00

English, 23.10.2020 14:00

Mathematics, 23.10.2020 14:00

Biology, 23.10.2020 14:00



Physics, 23.10.2020 14:00

English, 23.10.2020 14:00


English, 23.10.2020 14:00

Mathematics, 23.10.2020 14:00

Mathematics, 23.10.2020 14:00