Use the trick of Gauss to add up consecutive integers from 111 to 200200200, that is, find the sum 1+2+3+…+199+200 .\qquad\qquad\qquad 1+2+3+\ldots+199+200\;.1+2+3+…+199+ 200.

20100

Step-by-step explanation:

To find the sum of:

As per the trick of Gauss, let us divide the above terms in two halves.

and

Let us re rewrite the above terms by reversing the second sequence of terms.

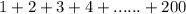
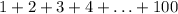 (it has 100 terms) and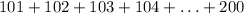

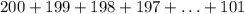(It also has 100 terms)

Adding the corresponding terms (it will also contain 100 terms):

1 + 200 = 201

2 + 199 = 201

3 + 198 = 201

:

:

100 + 101 = 201

The number of terms in each sequence are 100.

So, we have to add 201 for 100 times to get the required sum.

Required sum = 201 + 201 + 201 + 201 + . . . + 201  (100 times)

Required sum = 100 201 = 20100

d

step-by-step explanation:

answer is 12345678900987654321234567890987654321

step-by-step explanation: