Solve the given integral equation for LaTeX: y(t)y ( t ). LaTeX: y(t)+9\displaystyle{\int_{0}^{t}e^{ 9(t-v)}y(v)\, dv}=\sin(3t)y ( t ) + 9 ∫ 0 t e 9 ( t − v ) y ( v ) d v = sin ⁡ ( 3 t ) Group of answer choices LaTeX: y(t)=3\cos(3t)+9\sin(3t)-9 y ( t ) = 3 cos ⁡ ( 3 t ) + 9 sin ⁡ ( 3 t ) − 9 LaTeX: y(t)=3\cos(3t)+\sin(3t)-3 y ( t ) = 3 cos ⁡ ( 3 t ) + sin ⁡ ( 3 t ) − 3 LaTeX: y(t)=3\cos(3t)+\sin(3t) y ( t ) = 3 cos ⁡ ( 3 t ) + sin ⁡ ( 3 t ) LaTeX: y(t)=3\cos(3t)+9\sin(3t) y ( t ) = 3 cos ⁡ ( 3 t ) + 9 sin ⁡ ( 3 t ) LaTeX: y(t)=\cos(3t)+3\sin(3t)-3

Looks like the equation is

Differentiating both sides yields the linear ODE,

or

Multiply both sides by the integrating factor :

Integrate both sides, then solve for :

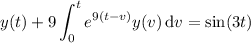
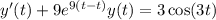
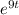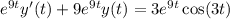
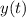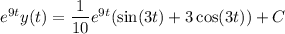
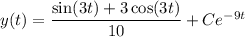
The given answer choices all seem to be missing C, so I suspect you left out an initial condition. But we can find one; let , then the integral vanishes and we're left with 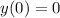. So

So the particular solution is

solve systems of equations by graphing. a system of linear equations contains two or more equations e.g. y=0.5x+2 and y=x-2. the solution of such a system is the ordered pair that is a solution to both equations. to solve a system of linear equations graphically we graph both equations in the same coordinate system

b is the correct answer