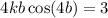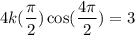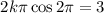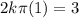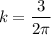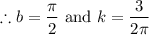Mathematics, 29.07.2020 03:01 cathydaves
Consider the curve of the form y(t) = ksin(bt2) . (a) Given that the first critical point of y(t) for positive t occurs at t = 1 tells us that y '(0) = 1 y(0) = 1 y '(1) = 0 y(1) = 0 Given that the derivative value of y(t) is 3 when t = 2 tells us that y '(3) = 2 y '(0) = 2 y '(2) = 0 y '(2) = 3 (b) Find dy dt = kcos(bt2)·b2t (c) Find the exact values for k and b that satisfy the conditions in part (a). Note: Choose the smallest positive value of b that works.

Answers: 1


Another question on Mathematics

Mathematics, 21.06.2019 19:30
When 142 is added to a number the result is 64 more then 3 times the number. option 35 37 39 41
Answers: 2

Mathematics, 21.06.2019 20:30
1) you deposit $2,500 in an account that earns 4% simple interest. how much do you earn in eight years?
Answers: 1

Mathematics, 22.06.2019 00:40
Which linear function represents the line given by the point-slope equation y + 1 = –3(x – 5)?
Answers: 1

You know the right answer?
Consider the curve of the form y(t) = ksin(bt2) . (a) Given that the first critical point of y(t) fo...
Questions

Biology, 29.08.2019 04:41

Mathematics, 29.08.2019 04:41




Biology, 29.08.2019 04:41


Biology, 29.08.2019 04:41

History, 29.08.2019 04:41




History, 29.08.2019 04:41

Physics, 29.08.2019 04:41





Mathematics, 29.08.2019 04:41

Mathematics, 29.08.2019 04:41

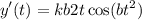
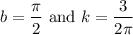
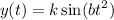
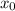 which lies in the domain of f where the derivative is 0.
which lies in the domain of f where the derivative is 0.![y'(t)=\frac{d}{dt}[k \sin (bt^2)]\\ y'(t)=k\frac{d}{dt}[\sin (bt^2)]](/tpl/images/0714/5492/bcd93.png)
![y'(t)=k \cos (bt^2)(\frac{d}{dt}[bt^2])\\ y'(t)=k\cos(bt^2)(b2t)\\ y'(t)= kb2t\cos(bt^2)](/tpl/images/0714/5492/e6dee.png)
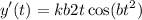
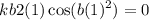
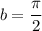
![$\therefore kb2(2)\cos [b(2)^2]=3$](/tpl/images/0714/5492/dd1ee.png)