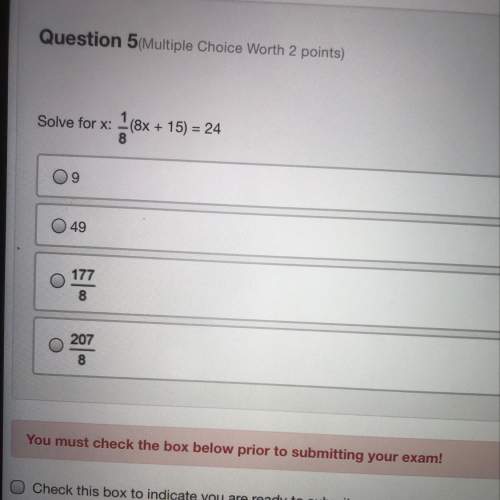
Mathematics, 24.06.2020 23:01 vanessacox45

Consider the diagram and the proof below. Given: In △ABC, AD ⊥ BC
Prove: StartFraction sine (uppercase B) Over b EndFraction = StartFraction sine (uppercase C) Over c EndFraction

Triangle A B C is shown. A perpendicular bisector is drawn from point A to point D on side C B forming a right angle. The length of A D is h, the length of C B is a, the length of C A is b, and the length of A B is c.

A 2-column table has 7 rows. The first column is labeled Statement with entries In triangle A B C line segment A D is perpendicular to line segment B C, In triangle A D B sine (uppercase B) = StartFraction h Over c EndFraction, c sine (uppercase B) = h, In triangle A C D, sine (uppercase C) = StartFraction h Over b EndFraction, b sine (uppercase C) = h, question mark, StartFraction sine (uppercase B) Over b EndFraction = StartFraction sine (uppercase C) Over c EndFraction. The second column is labeled Reason with entries given, definition of sine, multiplication property of equality, definition of sine, multiplication property of equality, substitution, and division property of equality.

What is the missing statement in Step 6?

b = c

StartFraction h Over b EndFraction = StartFraction h Over c EndFraction
csin(B) = bsin(C)

bsin(B) = csin(C)

Answers: 3

Show answers

Another question on Mathematics

Mathematics, 21.06.2019 19:00

Astore has clearance items that have been marked down by 60%. they are having a sale, advertising an additional 55% off clearance items. what percent of the original price do you end up paying?

Answers: 1

Answer

Mathematics, 21.06.2019 20:30

Secant be and cf intersect at point d inside a what is the measure of cde

Answers: 1

Answer

Mathematics, 21.06.2019 23:30

Aprisoner is trapped in a cell containing three doors. the first door leads to a tunnel that returns him to his cell after two days of travel. the second leads to a tunnel that returns him to his cell after three days of travel. the third door leads immediately to freedom. (a) assuming that the prisoner will always select doors 1, 2 and 3 with probabili- ties 0.5,0.3,0.2 (respectively), what is the expected number of days until he reaches freedom? (b) assuming that the prisoner is always equally likely to choose among those doors that he has not used, what is the expected number of days until he reaches freedom? (in this version, if the prisoner initially tries door 1, for example, then when he returns to the cell, he will now select only from doors 2 and 3.) (c) for parts (a) and (b), find the variance of the number of days until the prisoner reaches freedom. hint for part (b): define ni to be the number of additional days the prisoner spends after initially choosing door i and returning to his cell.

Answers: 1

Answer

Mathematics, 21.06.2019 23:40

Let x = a + bi and y = c + di and z = f + gi. which statements are true?

Answers: 1

Answer

You know the right answer?

Consider the diagram and the proof below. Given: In △ABC, AD ⊥ BC
Prove: StartFraction sine (...

Questions