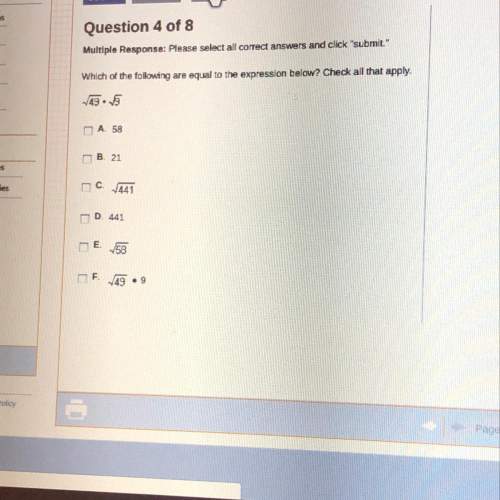
Mathematics, 10.06.2020 06:57 SavannahP04

Consider the incomplete paragraph proof. Given: Isosceles right triangle XYZ (45°–45°–90° triangle) Prove: In a 45°–45°–90° triangle, the hypotenuse is StartRoot 2 EndRoottimes the length of each leg. Triangle X Y Z is shown. Angle X Y Z is 90 degrees and the other 2 angles are 45 degrees. The length of X Y is a, the length of Y Z is a, and the length of X Z is c. Because triangle XYZ is a right triangle, the side lengths must satisfy the Pythagorean theorem, a2 + b2 = c2, which in this isosceles triangle becomes a2 + a2 = c2. By combining like terms, 2a2 = c2.

Which final step will prove that the length of the hypotenuse, c, is StartRoot 2 EndRoot times the length of each leg?

Substitute values for a and c into the original Pythagorean theorem equation. Divide both sides of the equation by two, then determine the principal square root of both sides of the equation.
Determine the principal square root of both sides of the equation.
Divide both sides of the equation by 2.

Answers: 1

Show answers

Another question on Mathematics

Mathematics, 21.06.2019 19:10

Revirite the formula to determine the area covered by one can of paint. alyssa and her father are going to paint the house this summer. they know they'll need 6 cans of paint. enter the correct answer. 000 done a formula that describes this scenario is (licierali 000 oo 6 w w = the total area of the walls p = area covered by a can of paint

Answers: 1

Answer

Mathematics, 21.06.2019 20:00

The two cylinders are similar. if the ratio of their surface areas is 9/1.44 find the volume of each cylinder. round your answer to the nearest hundredth. a. small cylinder: 152.00 m3 large cylinder: 950.02 m3 b. small cylinder: 972.14 m3 large cylinder: 12,924.24 m3 c. small cylinder: 851.22 m3 large cylinder: 13,300.25 m3 d. small cylinder: 682.95 m3 large cylinder: 13,539.68 m3

Answers: 2

Answer

Mathematics, 21.06.2019 22:20

Which strategy is used by public health to reduce the incidence of food poisoning?

Answers: 1

Answer

Mathematics, 22.06.2019 00:00

I've been working on this for a few days and i just don't understand, it's due in a few hours. you.the direction of a vector is defined as the angle of the vector in relation to a horizontal line. as a standard, this angle is measured counterclockwise from the positive x-axis. the direction or angle of v in the diagram is α.part a: how can you use trigonometric ratios to calculate the direction α of a general vector v = < x, y> similar to the diagram? part bsuppose that vector v lies in quadrant ii, quadrant iii, or quadrant iv. how can you use trigonometric ratios to calculate the direction (i.e., angle) of the vector in each of these quadrants with respect to the positive x-axis? the angle between the vector and the positive x-axis will be greater than 90 degrees in each case.part cnow try a numerical problem. what is the direction of the vector w = < -1, 6 > ?

Answers: 1

Answer

You know the right answer?

Consider the incomplete paragraph proof. Given: Isosceles right triangle XYZ (45°–45°–90° triangle)...

Questions