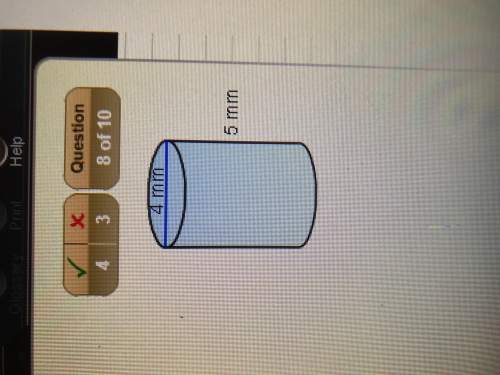
Mathematics, 09.06.2020 23:57 lbbeanss
C is the incenter of isosceles triangle ABD with vertex angle ∠ABD. Does the following proof correctly justify that triangles ABC and DBC are congruent?
It is given that C is the incenter of triangle ABD, so segment BC is an altitude of angle ABD.
Angles ABC and DBC are congruent according to the definition of an angle bisector.
Segments AB and DB are congruent by the definition of an isosceles triangle.
Triangles ABC and DBC share side BC, so it is congruent to itself by the reflexive property.
By the SAS postulate, triangles ABC and DBC are congruent.
Triangle ABD with segments BC, DC, and AC drawn from each vertex and meeting at point C inside triangle ABD.
There is an error in line 1; segment BC should be an angle bisector.
The proof is correct.
There is an error in line 3; segments AB and BC are congruent.
There is an error in line 5; the ASA Postulate should be used.

Answers: 3


Another question on Mathematics

Mathematics, 21.06.2019 16:30
Arandom sample of 150 high school students were asked whether they have a job. the results are shown in the table. have a job do not have a job male 48 35 female 41 26 select a ord or phrase from the drop-down menus to correctly complete the statements describing the association.
Answers: 1

Mathematics, 21.06.2019 19:00
Through non-collinear points there is exactly one plane.
Answers: 1

Mathematics, 21.06.2019 20:00
An investment decreases in value by 30% in the first year and decreases by 40% in the second year. what is the percent decrease in percentage in the investment after two years
Answers: 1

Mathematics, 21.06.2019 23:40
The function f(x)= -(x+5)(x+1) is down. what is the range of the function?
Answers: 3
You know the right answer?
C is the incenter of isosceles triangle ABD with vertex angle ∠ABD. Does the following proof correct...
Questions



Chemistry, 04.01.2020 04:31



Chemistry, 04.01.2020 04:31





History, 04.01.2020 04:31


English, 04.01.2020 04:31

Chemistry, 04.01.2020 04:31

Arts, 04.01.2020 04:31

Mathematics, 04.01.2020 04:31


Mathematics, 04.01.2020 04:31

Mathematics, 04.01.2020 04:31