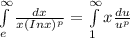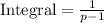Mathematics, 07.06.2020 04:01 igtguith
Find the values of p for which the following integral converges:
∫[infinity]e 1/(x(ln(x))^p)dx
Input youranswer by writing it as an interval. Enter brackets or parentheses in the first and fourth blanks as appropriate, and enter the interval endpoints in the second and third blanks. Use INF and NINF (in upper-case letters) for positive and negative infinity if needed. If the improper integral diverges for all p, type an upper-case "D" in every blank.
Values of p are in the interval ,
For the values of p at which the integral converges, evaluate it. Integral =

Answers: 1


Another question on Mathematics

Mathematics, 21.06.2019 16:30
Both the red and blue line segments stretch from the center of the circle to a point on the circle. the length of the blue segment is 5. how long is the red line segment?
Answers: 1

Mathematics, 21.06.2019 17:00
Two streets intersect at a 30- degree angle. at the intersection, the are four crosswalks formed that are the same length. what type of quadrilateral is formed by the crosswalks?
Answers: 3

Mathematics, 21.06.2019 18:10
Which of these sequences is a geometric sequence a 1,2,4, 7, 11, 16, 22. b. 2.4.8.14.22.38 c.3.6.9. 15.18,21 d. 3,9,27,81,243,729,
Answers: 1

Mathematics, 21.06.2019 20:00
Apatient is to be given 35 milligrams of demerol every 4 hours. you have demerol 50 milligrams/milliliter in stock. how many milliliters should be given per dose?
Answers: 2
You know the right answer?
Find the values of p for which the following integral converges:
∫[infinity]e 1/(x(ln(x))^p)dx
Questions


Social Studies, 13.10.2020 14:01


Mathematics, 13.10.2020 14:01





Chemistry, 13.10.2020 14:01


Social Studies, 13.10.2020 14:01

Health, 13.10.2020 14:01

Mathematics, 13.10.2020 14:01

History, 13.10.2020 14:01



English, 13.10.2020 14:01

History, 13.10.2020 14:01

English, 13.10.2020 14:01

Mathematics, 13.10.2020 14:01

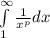
 and divertgent if p ≤ 1
and divertgent if p ≤ 1