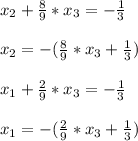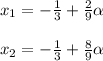Mathematics, 21.05.2020 04:03 lovvyDovvy04
Given the following system of equations:
6X1 - 6x2 - 4x3 = 0
X1 - 7x2 - 6x3 = 2
X1 +5x2 + nx3 = -2
Rewrite the system in Ax = b format and determine the following:
a. By reduction of the augmented matrix [A|b] to ref, find a value for n such that the system is consistent with an infinite number of solutions.
b. Based on your solution in part A, identify the rank of matrix A and rank of the augmented matrix [A|b].
c. Based on the value of the rank, how many equations (the row vectors of the augmented matrix [Ab]) are linearly independent?
d. Using your solution in part A, solve the system of equations using Gauss-jordan elimination.

Answers: 2


Another question on Mathematics

Mathematics, 21.06.2019 15:30
Two blends of tea are mixed to make a blend that will be sold at the fair. black tea sells for $2.20 per pound and orange pekoe tea sells for $3.00 per pound. how much of each should be used to obtain a 4lb blend selling for $2.50 per pound?
Answers: 1

Mathematics, 21.06.2019 15:30
Diane owes $387 to her brother. if she debits her bank account $161.25 a month to pay him back, how many months will it take her to pay off the debt?
Answers: 2

Mathematics, 21.06.2019 15:30
Maria donates a fixed amount, a, to a charity each month. if she donates $300 in 12 months, what is the equation for a? a. a + 300 = 12 b. a × 300 = 12 c. a × 12 = 300 d. a + 12 = 300 e. a + 32 = 100
Answers: 3

Mathematics, 21.06.2019 16:00
The graph shows the distance y, in inches, a pendulum moves to the right (positive displacement) and to the left (negative displacement), for a given number of seconds x. how many seconds are required for the pendulum to move from its resting position and return? enter your answer in the box.
Answers: 2
You know the right answer?
Given the following system of equations:
6X1 - 6x2 - 4x3 = 0
X1 - 7x2 - 6x3 = 2...
6X1 - 6x2 - 4x3 = 0
X1 - 7x2 - 6x3 = 2...
Questions





Biology, 06.10.2019 20:30

English, 06.10.2019 20:30


English, 06.10.2019 20:30

Mathematics, 06.10.2019 20:30





Mathematics, 06.10.2019 20:30

Mathematics, 06.10.2019 20:30

Health, 06.10.2019 20:30


History, 06.10.2019 20:30

Social Studies, 06.10.2019 20:30

World Languages, 06.10.2019 20:30

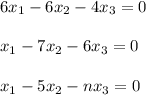
![A = \left[\begin{array}{ccc}a_1_1&a_1_2&a_1_3\\a_2_1&a_2_2&a_2_3\\a_3_1&a_3_2&a_3_3\end{array}\right]](/tpl/images/0658/4969/0e336.png)
![A = \left[\begin{array}{ccc}6&-6&-4\\1&-7&-6\\1&5&n\end{array}\right]](/tpl/images/0658/4969/6e56f.png)
![X = \left[\begin{array}{c}x_1&x_2&x_3\end{array}\right]](/tpl/images/0658/4969/e15f5.png)
![b = \left[\begin{array}{c}0&2&-2\end{array}\right]](/tpl/images/0658/4969/21eb9.png)
![A*X = b\\\\\left[\begin{array}{ccc}6&-6&-4\\1&-7&-6\\1&5&n\end{array}\right]*\left[\begin{array}{c}x_1&x_2&x_3\end{array}\right] = \left[\begin{array}{c}0&2&-2\end{array}\right]](/tpl/images/0658/4969/9565d.png)
![[ A | b ]\\\\ \left[\begin{array}{ccccc}6&-6&-4&|&0\\1&-7&-6&|&2\\1&5&n&|&-2\end{array}\right]](/tpl/images/0658/4969/febbd.png)
![\left[\begin{array}{ccccc}1&-1&-\frac{2}{3} &|&0\\1&-7&-6&|&2\\0&12&n+6&|&-4\end{array}\right]](/tpl/images/0658/4969/9f396.png)
![\left[\begin{array}{ccccc}1&-1&-\frac{2}{3} &|&0\\0&-6&-\frac{16}{3} &|&2\\0&1&\frac{n+6}{12} &|&-\frac{1}{3}\end{array}\right]](/tpl/images/0658/4969/91dee.png)
![\left[\begin{array}{ccccc}1&-1&-\frac{2}{3} &|&0\\0&-1&-\frac{8}{9} &|&\frac{1}{3} \\0&1&\frac{n+6}{12} &|&-\frac{1}{3}\end{array}\right]](/tpl/images/0658/4969/786ad.png)
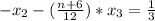

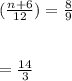
![\left[\begin{array}{ccccc}1&-1&-\frac{2}{3} &|&0\\0&1&\frac{8}{9} &|&-\frac{1}{3} \\0&0&0 &|&0\end{array}\right]](/tpl/images/0658/4969/91da5.png)
![\left[\begin{array}{ccccc}1&0&\frac{2}{9} &|&-\frac{1}{3} \\0&1&\frac{8}{9} &|&-\frac{1}{3} \\0&0&0 &|&0\end{array}\right]](/tpl/images/0658/4969/75515.png)