Consider the following proposed proof, which claims to show that every nonnegative integer power of every nonzero real number is 1.
Let r be any nonzero real number, and let P(n) be the equation r ^n = 1.
Show that P(0) is true : P(0) is true because r^0 = 1 by definition of zeroth power.
Show that for every integer k >= 0, if P(i) is true for each integer i from 0 through k, then P(k + 1) is also true:
Let k be any integer with k >= 0 and suppose that r^ i = 1 for each integer i from 0 through k. This is the inductive hypothesis. We must show that r^ k + 1 = 1. Now
r^ k + 1 = r^ k + k - (k - 1) because k + k - (k - 1) = k + 1
r ^k * r^ k / r^ k - 1 by the laws of exponents
1*1 / 1 by inductive hypothesis
=1
Thus r^ k + 1 = 1 [as was to be shown].
[Since we have proved the basis step and the inductive step of the strong mathematical induction, we conclude that the given statement is true.]
Question:
a) Identify the error(s) in the above "proof."

The statement is not true. There is an error in the following step:

Step-by-step explanation:

Here is the complete proof:

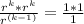
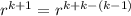 (because k + k - (k - 1) = k + 1)

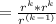(By laws of exponent)

(Since the power of r is a negative integer i.e. -1 it will shift to the numerator)

 (We get this equation after canceling out the similar terms in numerator and denominator in previous step)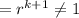

(Provided r > 1 or r < -1)

c.   x=2.4cm

step-by-step explanation:

similar triangles are triangles which have the same shape but not the same size. this means their angle measures are equal but their side lengths are not instead they are proportional. to solve, we will set up a proportion and solve.

a proportion is two equal ratios set equal to each other. we form the ratios by finding corresponding sides (sides which match to each other on both triangles by their position). out ratios will be one side of the small triangle over the corresponding side on the big triangle as shown below:

.

to solve the proportion, we'll cross multiply by multiplying numerator with denominator across the equal sign.

2.2°  

step-by-step explanation:

let θ = the angle of elevation.

tanθ =77/2020

tanθ = 0.038 12

      θ = tan⁻¹0.038 12

      θ = 2.2°