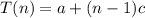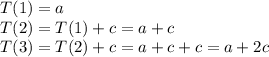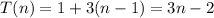Mathematics, 05.05.2020 15:59 jetblackcap
A family of recurrences has the following form for constants a and c: T(1) = a T(n) = T(n-1) + c for n > 1 Solve this recurrence for T(n) in terms of a and c. Then demonstrate that you have the solution by identifying, from the list below, the correct formula for T(n) in terms of specific values of a and c. a) If a=1 and c=3, then T(n) is 3n - 2. b) If a=1 and c=3, then T(n) is n + 2. c) If a=3 and c=5, then T(n) is 3n + 2. d) If a=3 and c=5, then T(n) is 5n + 3.'

Answers: 2


Another question on Mathematics

Mathematics, 21.06.2019 20:00
Worth 30 points! in this diagram, both polygons are regular. what is the value, in degrees, of the sum of the measures of angles abc and abd?
Answers: 2

Mathematics, 21.06.2019 22:30
Reinel saves 30% of every pay check. his paycheck last week was 560$. how much did reniel save last week?
Answers: 2

Mathematics, 22.06.2019 02:30
Solve the system of equations. 2x-2y=-4 and x+y=8. show work
Answers: 1

Mathematics, 22.06.2019 04:00
Sarah needs 3 feet of fabric for a project she is working on, but the store only sells the fabric in meters. one meter of fabric costs $1.20. how much will the fabric cost?
Answers: 2
You know the right answer?
A family of recurrences has the following form for constants a and c: T(1) = a T(n) = T(n-1) + c for...
Questions


Mathematics, 11.10.2019 20:30


Social Studies, 11.10.2019 20:30

Chemistry, 11.10.2019 20:30

History, 11.10.2019 20:30

Mathematics, 11.10.2019 20:30



Spanish, 11.10.2019 20:30




Mathematics, 11.10.2019 20:30





History, 11.10.2019 20:30

History, 11.10.2019 20:30