
Mathematics, 22.04.2020 04:40 Braxtonw875
Approximate f by a Taylor polynomial with degree n at the number a. Step 1 The Taylor polynomial with degree n = 3 is T3(x) = f(a) + f '(a)(x − a) + f ''(a) 2! (x − a)2 + f '''(a) 3! (x − a)3. The function f(x) = e2x2 has derivatives f '(x) = $$4x e2x2, f ''(x) = $$16x2+4 e2x2, and f '''(x) = $$48x+64x3 e2x2. Step 3 Therefore, T3(x) = . Submit Skip (you cannot come back)

Answers: 3


Another question on Mathematics

Mathematics, 21.06.2019 13:30
What value is equivalent to 5 + [5 × (4 + 2)]? a) 35 b) 45 c) 60 d) 110
Answers: 2

Mathematics, 21.06.2019 16:50
Before simplifying, how many terms are there in the expression 2x - 5y + 3 + x?
Answers: 1


Mathematics, 21.06.2019 19:00
The weekly revenue for a company is r = 3p^2 + 60p + 1060, where p is the price of the company's product. what price will result in a revenue of $1200.
Answers: 1
You know the right answer?
Approximate f by a Taylor polynomial with degree n at the number a. Step 1 The Taylor polynomial wit...
Questions


Biology, 26.05.2021 16:10



Mathematics, 26.05.2021 16:10




Mathematics, 26.05.2021 16:10


Biology, 26.05.2021 16:10

English, 26.05.2021 16:10

Mathematics, 26.05.2021 16:10

Mathematics, 26.05.2021 16:10

English, 26.05.2021 16:10


Mathematics, 26.05.2021 16:10


Mathematics, 26.05.2021 16:10

Mathematics, 26.05.2021 16:10

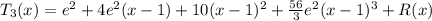
 is the error.
is the error. 
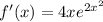 (This comes from the chain rule )
(This comes from the chain rule )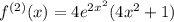 (This comes from the chain rule and the product rule)
(This comes from the chain rule and the product rule)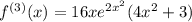 (This comes from the chain rule and the product rule)
(This comes from the chain rule and the product rule)

