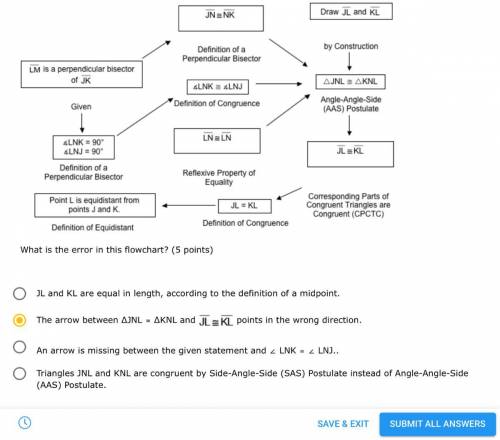
The following is an incorrect flowchart proving that point L, lying on line LM which is a perpendicular bisector of segment JK , is equidistant from points J and K:

Segment JK intersects line LM at point N

Line LM is a perpendicular bisector of segment JK, Given. Two arrows are drawn from this statement to the following two stateme

What is the error in this flowchart? (5 points)

JL and KL are equal in length, according to the definition of a midpoint.

The arrow between ΔJNL ≅ ΔKNL and segment J L is congruent to segment K L points in the wrong direction.

An arrow is missing between the given statement and ∠ LNK ≅ ∠ LNJ..

Triangles JNL and KNL are congruent by Side-Angle-Side (SAS) Postulate instead of Angle-Angle-Side (AAS) Postulate.

infinitely many solutions

step-by-step explanation:

we have been given the equation;

2(2x + 3) = -4 + 2(2x + 5)

we need to determine the value of x.

2(2x + 3), we expand this expression to obtain 4x + 6

similarly 2(2x + 5) will become 4x + 10

now we have;

4x + 6 = -4 + 4x + 10

4x + 6 = 4x + 10 - 4

4x + 6 = 4x + 6

the expression on the left hand side is identical to the one on the right hand side. therefore, we are looking at just a single straight line whose equation is;

y = 4x + 6

consequently, we shall have infinitely many solutions

the revenue of the fitness center, y, is the product of two factors: the number of members and the fee paid by each member. there are 320 members now, but number of members goes down by 10 for each $5 increase in fees, so if x is the number of $5 price increases then members is equal to (320 - 10x). since the fee is currently $45, and the fee increases by $5 for every price bump x, the fee is given by (45 + 5x). so, revenue y is given by y = (320 - 10x)(45 + 5x).

the answer is b.6

step-by-step explanation:

-8,5

step-by-step explanation: