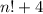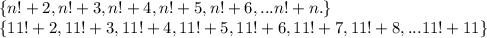Mathematics, 18.04.2020 04:32 haleylayne74
Let n be any natural number greater than 1. Explain why the numbers n! 2, n! 3, n! 4, ..., n! n must all be composite. (This exercise shows that it is possible to find arbitrarily long sequences of consecutive composite numbers.)

Answers: 2


Another question on Mathematics

Mathematics, 21.06.2019 14:30
Use the radius you found in part i (r=26.8 cm) with the surface area formula below to find the surface area of the sphere. show your work and round your answer to the nearest tenth. the surface area of a sphere: sa = 4πr^2 self note: 3.8.4
Answers: 2


Mathematics, 21.06.2019 22:00
What is the solution to the equation e3x=12? round your answer to the nearest hundredth
Answers: 1

Mathematics, 21.06.2019 22:20
The figure shows triangle def and line segment bc, which is parallel to ef: triangle def has a point b on side de and point c on side df. the line bc is parallel to the line ef. part a: is triangle def similar to triangle dbc? explain using what you know about triangle similarity. part b: which line segment on triangle dbc corresponds to line segment ef? explain your answer. part c: which angle on triangle dbc corresponds to angle f? explain your answer. asap
Answers: 3
You know the right answer?
Let n be any natural number greater than 1. Explain why the numbers n! 2, n! 3, n! 4, ..., n! n must...
Questions



Mathematics, 06.03.2021 15:10


Mathematics, 06.03.2021 15:10

Mathematics, 06.03.2021 15:20

Biology, 06.03.2021 15:20



Mathematics, 06.03.2021 15:20


Mathematics, 06.03.2021 15:20

Mathematics, 06.03.2021 15:20

Mathematics, 06.03.2021 15:20



English, 06.03.2021 15:20

English, 06.03.2021 15:20

Mathematics, 06.03.2021 15:20

English, 06.03.2021 15:20

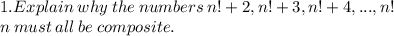
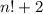
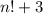 and
and