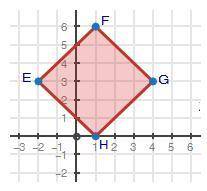
Ivan used coordinate geometry to prove that quadrilateral EFGH is a square.

Figure EFGH is shown. E is at negative 2, 3. F is at 1, 6. G is at 4, 3. H is at 1, 0.

Statement Reason
1. Quadrilateral EFGH is at E (−2, 3), F (1, 6), G (4, 3), and H (1, 0) 1. Given
2.__?__ 2.segment EF
E (−2, 3) F (1, 6)
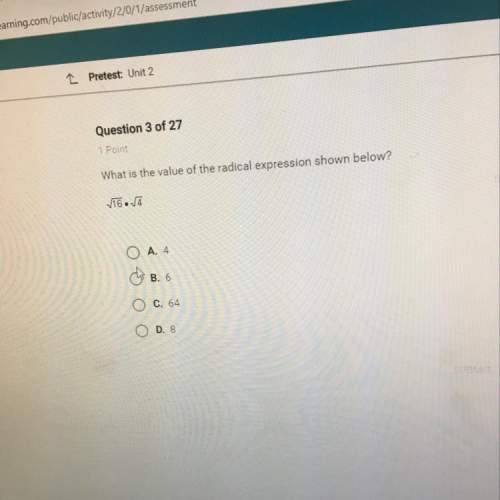
d equals the square root of the quantity 1 plus 2 all squared plus 6 minus 3 all squared
d equals the square root of the quantity 3 squared plus 3 squared equals the square root of 18 equals 3 times the square root of 2

segment FG
F (1, 6) G (4, 3)
d equals the square root of the quantity 4 minus 1 all squared plus 3 minus 6 all squared
d equals the square root of the quantity 3 squared plus negative 3 squared equals the square root of 18 equals 3 times the square root of 2 segment GH
G (4, 3) H (1, 0)
d equals the square root of the quantity 1 minus 4 all squared plus 0 minus 3 all squared
d equals the square root of the quantity negative 3 squared plus negative 3 squared equals the square root of 18 equals 3 times the square root of 2

segment EH
E (−2, 3) H (1, 0)
d equals the square root of the quantity 1 plus 2 all squared plus 0 minus 3 all squared
d equals the square root of the quantity 3 squared plus negative 3 squared equals the square root of 18 equals 3 times the square root of 2
3. segment EF is parallel to segment GH 3. segment EF
E (−2, 3) F (1, 6)
m equals 6 minus 3 over 1 plus 2 equals 3 over 3 equals 1 segment GH
G (4, 3) H (1, 0)
m equals 0 minus 3 over 1 minus 4 equals negative 3 over negative 3 equals 1
4. __?__ 4. segment EH
E(−2, 3) H (1, 0)
m equals 0 minus 3 over 1 plus 2 equals negative 3 over 3 equals negative 1 segment FG
F (1, 6) G (4, 3)
m equals 3 minus 6 over 4 minus 1 equals negative 3 over 3 equals negative 1
5. segment EF and segment GH are perpendicular to segment FG 5. The slope of segment EF and segment GHis 1. The slope of segment FG is −1.
6. __?__ 6. The slope of segment FG and segment EH is −1. The slope of segment GH is 1.
7. Quadrilateral EFGH is a square 7. All sides are congruent, opposite sides are parallel, and adjacent sides are perpendicular.

Which of the following completes statement 4 of the proof?
segment EF, segment FG, segment GH, and segment EH are congruent
segment EF is parallel to segment GH
segment EH is parallel to segment FG
segment FGand segment EH are perpendicular to segment GH