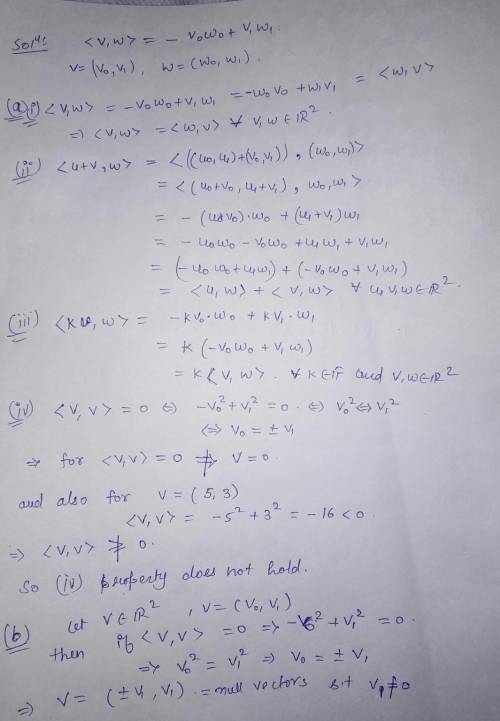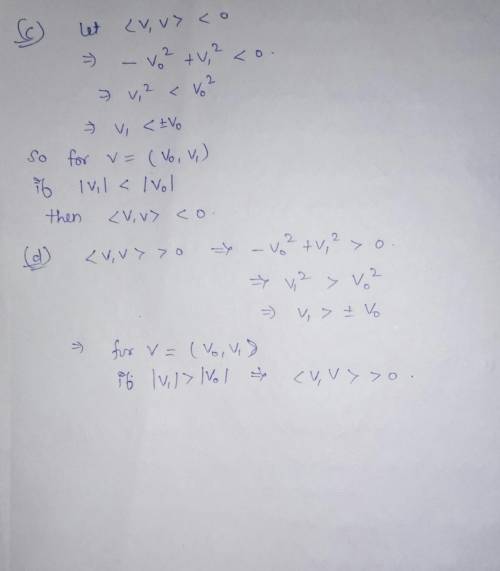Toying with Spacetime Consider the two dimensional vector space R2, endowed with an inner product given by (v. w) = -20W + vw1 for all vectors v = (10.01) and w = (wo, w.). This is called a pseudo-inner product on R2 and, when gen- eralized to R, is of fundamental importance in Einstein's special theory of relativity. More specifically, two-dimensional Minkowski spacetime, often denoted by Ri, has this metric structure with the zeroth- component denoting time), and it is called a toy spacetime since it resembles our actual four-dimensional spacetime with fewer spatial dimensions. Though not realistic, it can make some calculations easier to do, whence the descriptor "toy" in its name. (a) Show this inner product satisfies all the criteria of an inner product except the positive-definite property, (uu) > 0. (b) Determine all nonzero vectors satisfying (v, v) = 0. Such vectors are called null vectors (c) Determine all vectors satisfying (v. v) <0. Such vectors are called timelike vectors. (d) Determine all vectors satisfying (v, v) > 0. Such vectors are called spacelike vectors. (e) Make a sketch of Rſ and indicate the position of the null, timelike, and spacelike vectors.

Lines b and c are parallel. what is the measure of 2? m2 = 31° m2 = 50° m2 = 120° m2 = 130°

In order to be invited to tutoring or extension activities a students performance 20 point higher or lower than average for the

(c) compare the results of parts (a) and (b). in general, how do you think the mode, median, and mean are affected when each data value in a set is multiplied by the same constant? multiplying each data value by the same constant c results in the mode, median, and mean increasing by a factor of c. multiplying each data value by the same constant c results in the mode, median, and mean remaining the same. multiplying each data value by the same constant c results in the mode, median, and mean decreasing by a factor of c. there is no distinct pattern when each data value is multiplied by the same constant. (d) suppose you have information about average heights of a random sample of airline passengers. the mode is 65 inches, the median is 72 inches, and the mean is 65 inches. to convert the data into centimeters, multiply each data value by 2.54. what are the values of the mode, median, and mean in centimeters? (enter your answers to two decimal places.) mode cm median cm mean cm in this problem, we explore the effect on the mean, median, and mode of multiplying each data value by the same number. consider the following data set 7, 7, 8, 11, 15. (a) compute the mode, median, and mean. (enter your answers to one (1) decimal places.) mean value = median = mode = (b) multiply 3 to each of the data values. compute the mode, median, and mean. (enter your answers to one (1) decimal places.) mean value = median = mode = --