
Mathematics, 12.03.2020 03:10 ecenteno2004
Find the arc length parameter along the given curve from the point where t=0 by evaluating the integral s(t)=lv(t)ldt
Then find the length of indicated portion of the curve r(t)= 5costi+5sintj+8tk, where 0<_t<_pi
The arc length parameter along the curve, starting at t=0 is s(t)=. (Type exact answers, using radicals as needed)
The length of the indicated portion of the curve is L=___. (Type exact answers, using radicals and Pi as needed)
Find the arc length parameter along the given curve from the point where t=0 by evaluating the integral s(t)=lv(t)ldt
Then find the length of indicated portion of the curve r(t)=(2e^tcost)i+(2e^tsint)j-2e^tk, -ln4<_t<_0 s(t)=__ (Type exact answers, using radicals as needed)
The length of rage indicated portion of the curve is __ units. (Type exact answers, using radicals as needed)

Answers: 2


Another question on Mathematics

Mathematics, 21.06.2019 19:30
Me. i can't figure out this question. give an explanation too. .
Answers: 1

Mathematics, 21.06.2019 20:00
In new york city at the spring equinox there are 12 hours 8 minutes of daylight. the longest and shortest days of the year very by two hours and 53 minutes from the equinox in this year the equinox falls on march 21 in this task you use trigonometric function to model the hours of daylight hours on certain days of the year in new york city a.what is the independent and dependent variables? b.find the amplitude and the period of the function. c.create a trigonometric function that describes the hours of sunlight for each day of the year. d. graph the function you build in part c. e. use the function you build in part c to find out how many fewer daylight hours february 10 will have than march 21. you may look at the calendar.
Answers: 1

Mathematics, 21.06.2019 20:00
Ahiker stands at an unknown elevation before he ascends 2 miles up a mountain to an elevation of 9 miles. find the elevation of the hiker before his ascent.
Answers: 1

Mathematics, 22.06.2019 01:30
The diameter of the moon is about 3500 km. approximate the surface area of the moon using the formula for the surface area of a sphere, s = 4? r^2. write your answer in scientific notation.
Answers: 3
You know the right answer?
Find the arc length parameter along the given curve from the point where t=0 by evaluating the integ...
Questions






Biology, 06.10.2019 09:01



Mathematics, 06.10.2019 09:01

Mathematics, 06.10.2019 09:01




Mathematics, 06.10.2019 09:01

Computers and Technology, 06.10.2019 09:01

Mathematics, 06.10.2019 09:01

Mathematics, 06.10.2019 09:01

English, 06.10.2019 09:01


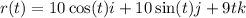 where
where 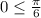
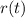 with respect to
with respect to 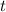
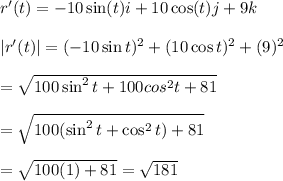
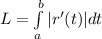
![s(t)=\int\limits^b_a|v(\tau)|dt\\\\=\int\limits^{\frac{\pi}{6}}_a\sqrt{181}dt\, since\, |v|=|r'(t)|\, or\, |v|=\sqrt{181}\\\\=\sqrt{181}[t]\limits^{\frac{\pi}{6}}_0\\\\=\sqrt{181}[\frac{\pi}{6}-0]\\\\=\frac{\sqrt{181\times \pi}}{6}=7.0443](/tpl/images/0544/2333/54026.png)



