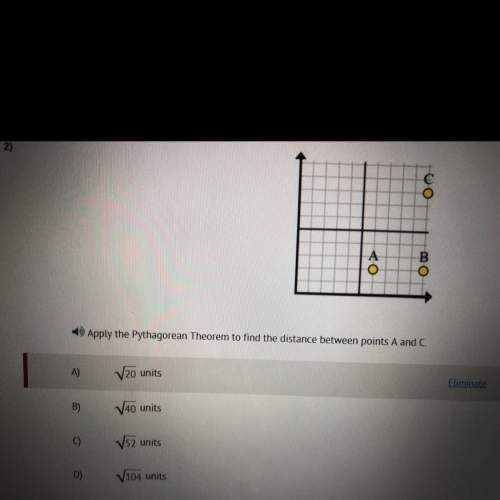
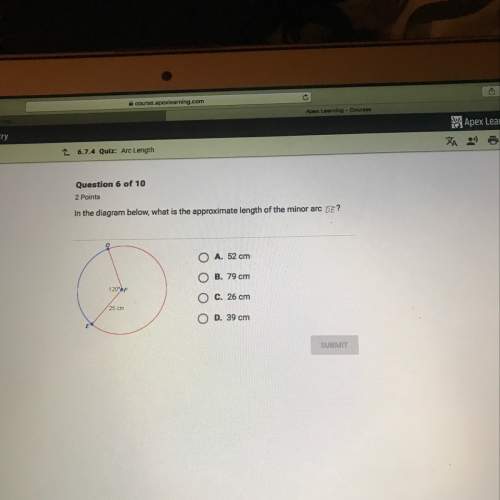
Mathematics, 03.03.2020 00:57 Jasten
Video Example EXAMPLE 3 (a) Use the Midpoint Rule with n = 10 to approximate the integral 1 0 ex2 dx. (b) Give an upper bound for the error involved in this approximation. SOLUTION (a) Since a = 0, b = 1, and n = 10, the Midpoint Rule gives the following. (Round your answer to six decimal places.) 1 0 ex2 dx ≈ Δx[f(0.05) + f(0.15) + ... + f(0.85) + f(0.95)] = 0.1 e0.0025 + e0.0225 + e0.0625 + e0.1225 + e0.2025 + e0.3025 + e0.4225 + e0.5625 + e0.7225 + e0.9025

Answers: 3


Another question on Mathematics

Mathematics, 21.06.2019 17:20
Which of these equations, when solved, gives a different value of x than the other three? a9.1 = -0.2x + 10 b10 = 9.1 + 0.2x c10 – 0.2x = 9.1 d9.1 – 10 = 0.2x
Answers: 1


Mathematics, 21.06.2019 22:50
Which of the following is closest to 32.9 x 7.5? a: 232 b: 259 c: 220 d: 265
Answers: 2

You know the right answer?
Video Example EXAMPLE 3 (a) Use the Midpoint Rule with n = 10 to approximate the integral 1 0 ex2 dx...
Questions


Chemistry, 10.10.2019 02:00



Biology, 10.10.2019 02:00

Social Studies, 10.10.2019 02:00


Mathematics, 10.10.2019 02:00









History, 10.10.2019 02:00


English, 10.10.2019 02:00