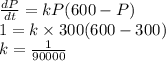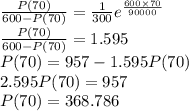Mathematics, 12.02.2020 03:18 Aliyahh5988
Suppose that the population P(t) of a country satisfies the differential equation dP/dt = kP (600 - P) with k constant. Its population in 1960 was 300 million and was then growing at the rate of 1 million per year. Predict this country's population for the year 2030.

Answers: 3


Another question on Mathematics

Mathematics, 21.06.2019 15:50
Name the most appropriate metric unit for each measurement
Answers: 3



You know the right answer?
Suppose that the population P(t) of a country satisfies the differential equation dP/dt = kP (600 -...
Questions

Physics, 23.09.2020 23:01


Mathematics, 23.09.2020 23:01

History, 23.09.2020 23:01

Mathematics, 23.09.2020 23:01

Mathematics, 23.09.2020 23:01



Mathematics, 23.09.2020 23:01

Biology, 23.09.2020 23:01


Mathematics, 23.09.2020 23:01


Biology, 23.09.2020 23:01

English, 23.09.2020 23:01


Biology, 23.09.2020 23:01


English, 23.09.2020 23:01

Mathematics, 23.09.2020 23:01

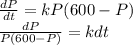
![\int\limits {\frac{1}{P(600-P)} } \, dP =k\int\limits {1} \, dt \\(\frac{1}{600} )[(\int\limits {\frac{1}{P} } \, dP) - (\int\limits {\frac{}{600-P} } \, dP)]=k\int\limits {1} \, dt\\\ln P-\ln (600-P)=600kt+C\\\ln (\frac{P}{600-P} )=600kt+C\\\frac{P}{600-P} = Ce^{600kt}](/tpl/images/0507/9481/33846.png)
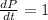 .
.