Show that if x is a geometric random variable with parameter p, then

e[1/x]= −p log(p)/(1−p)
hint: you will need to evaluate an expression of the form
i=1➝[infinity]∑(ai/ i)
to do so, write
ai/ i=0➝a∫(xi−1) dx then interchange the sum and the integral.

Step-by-step explanation:

The geometric distribution represents "the number of failures before you get a success in a series of Bernoulli trials. This discrete probability distribution is represented by the probability density function:"

Let X the random variable that measures the number os trials until the first success, we know that X follows this distribution:

In order to find the expected value E(1/X) we need to find this sum:

Lets consider the following series:

And let's assume that this series is a power series with b a number between (0,1). If we apply integration of this series we have this:

  (a)

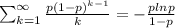
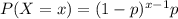
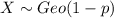
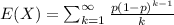
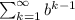
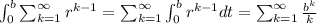On the last step we assume that and 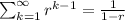, then the integral on the left part of equation (a) would be 1. And we have: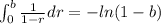

And for the next step we have:

And with this we have the requiered proof.

And since we have that:

oof

step-by-step explanation:

77

step-by-step explanation: