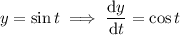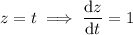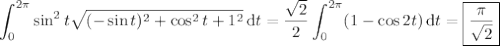Mathematics, 26.11.2019 05:31 townselt3861
Evaluate ∫c ysin(z)ds, where c is the circular helix given by the equations x = cos(t), y = sin(t), z = t, 0 ≤ t ≤ 2π. solution the formula for a line integral in space gives the following. ∫y sin(z)ds = sin2(t) dt = (sin(t))2√ (cos(t))2 + (sin(t))2 + 1dt = 1 2 (1 - cos(2t))dt = √2 2 =

Answers: 2


Another question on Mathematics

Mathematics, 21.06.2019 13:00
X+ y = k 2x + 3y = k + 1 the point of intersection of the lines has an x-coordinate of a.2k + 1 b.-2k + 1 c.2k - 1
Answers: 1

Mathematics, 21.06.2019 22:00
Which of the following graphs could represent a cubic function?
Answers: 1

Mathematics, 21.06.2019 22:10
Which function can be used to model the monthly profit for x trinkets produced? f(x) = –4(x – 50)(x – 250) f(x) = (x – 50)(x – 250) f(x) = 28(x + 50)(x + 250) f(x) = (x + 50)(x + 250)
Answers: 2

Mathematics, 21.06.2019 23:00
Which of the following graphs could represent a cubic function?
Answers: 1
You know the right answer?
Evaluate ∫c ysin(z)ds, where c is the circular helix given by the equations x = cos(t), y = sin(t),...
Questions

History, 15.04.2021 18:50

Computers and Technology, 15.04.2021 18:50

Chemistry, 15.04.2021 18:50

Mathematics, 15.04.2021 18:50

Mathematics, 15.04.2021 18:50

Mathematics, 15.04.2021 18:50

Chemistry, 15.04.2021 18:50

History, 15.04.2021 18:50




Mathematics, 15.04.2021 18:50

Mathematics, 15.04.2021 18:50

Social Studies, 15.04.2021 18:50

Mathematics, 15.04.2021 18:50

Mathematics, 15.04.2021 18:50



Mathematics, 15.04.2021 18:50