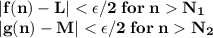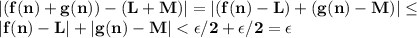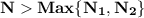Mathematics, 10.11.2019 02:31 pakabigail4796
Given a sequence f: z+→r of real numbers, we say that the sequence converges to a real number l if for all ε> 0, there exists a positive integer n such that for any positive integer n, if n≥n, then |f(n)-l|< ε. prove that if a sequence f converges to l and a sequence g converges to m, then the sequence f+g converges to l+m. (you may use the triangle inequality: |a+b|≤|a|+|b| for any real numbers a and b.)

Answers: 2


Another question on Mathematics

Mathematics, 21.06.2019 18:00
Ray ce is the angle bisector of zacd, which statement about the figure must be true? mzecd-mzecb mzace « 4mzacd zace - zdcb zecd zacd save and exit
Answers: 1

Mathematics, 21.06.2019 20:00
You have 138.72 in your saving account u take out 45.23 and 18.00 you deposit 75.85 into your account
Answers: 1

Mathematics, 21.06.2019 21:10
Jenny earned a 77 on her most recent test jenny score is no less then 5 points greater then 4/5 of terrance’s score if t represents terrance score which inequality represents the situation
Answers: 3

You know the right answer?
Given a sequence f: z+→r of real numbers, we say that the sequence converges to a real number l if f...
Questions

Physics, 04.10.2019 20:00

Geography, 04.10.2019 20:00


Mathematics, 04.10.2019 20:00

Health, 04.10.2019 20:00

Mathematics, 04.10.2019 20:00

Biology, 04.10.2019 20:00

Biology, 04.10.2019 20:00

History, 04.10.2019 20:00



Mathematics, 04.10.2019 20:00


Geography, 04.10.2019 20:00

History, 04.10.2019 20:00


Mathematics, 04.10.2019 20:00

Mathematics, 04.10.2019 20:00

Mathematics, 04.10.2019 20:00

 there exists
there exists  and
and 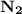 such that
such that