Mathematics, 17.10.2019 20:30 carolelai08
Chapter 15, section 15.3, question 023 a cobb-douglas production function p(k, l) and budget b(k, l) are given, where k represents capital and l represents labor. use lagrange multipliers to find the values of k and l that minimize budget given a production constraint. then give the value for 2 and choose its correct meaning. minimize budget: b = 4k + l production constraint: p = k1/2112 = 180 the values that minimize budget are k = number and l = number the value of l is number the value of a tells us that o for one extra unit increase in budget, we get an increase of 1/2 units in production. o for one extra unit increase in budget, we get an increase of 2 units in production. o for one extra unit increase in production, we get an increase of 1/2 units in budget. o for one extra unit increase in production, we get an increase of 1 units in budget.

Answers: 2


Another question on Mathematics

Mathematics, 21.06.2019 18:00
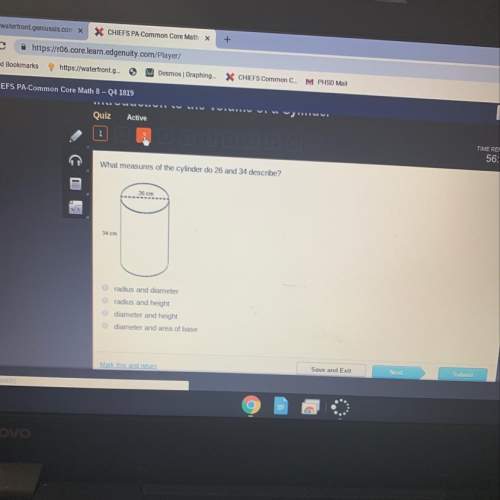
What is the measure of the smallest angle in the diagram? 15 29 32 45
Answers: 2

Mathematics, 21.06.2019 19:00
Arestaurant chef made 1 1/2 jars of pasta sauce. each serving of pasta requires 1/2 of a jar of sauce. how many servings of pasta will the chef be bale to prepare using the sauce?
Answers: 3

Mathematics, 21.06.2019 21:00
A.s.a.! this is a similarity in right triangles. next (solve for x)a.) 12b.) 5c.) 12.5d.) [tex] 6\sqrt{3} [/tex]
Answers: 2

Mathematics, 21.06.2019 23:30
Petes dog weighed 30 pounds it then lost 16% of it's weight how much did pete lose
Answers: 2
You know the right answer?
Chapter 15, section 15.3, question 023 a cobb-douglas production function p(k, l) and budget b(k, l)...
Questions













History, 14.04.2020 23:33


Computers and Technology, 14.04.2020 23:33



Social Studies, 14.04.2020 23:33


Biology, 14.04.2020 23:33