
Mathematics, 13.07.2019 00:30 kierraivey
Breaking stuff let {xi} n i=1 be a sample of random variables of size n with the property that xi ∼ n (µ, σ2 ) and cov(xi , xj ) = ρσ for all pairs i, j. a. solve for the mean and variance of x¯. b. what happens to the variance of x¯ as n → ∞? c. why do the clt and lln fail in this situation? d. using the provided code, simulate s = 1000 values of x¯ for n = 50, 100, 500. in all three cases calculate the mean and variance of the resulting distribution. create histograms for each. in this code, σ = 1 and ρ = .4. how does the variance for each n compare to the formula from part (a)?

Answers: 1


Another question on Mathematics


Mathematics, 21.06.2019 19:00
Write the pair of fractions as a pair of fractions with a common denominator
Answers: 3

Mathematics, 21.06.2019 19:30
Can someone me with the property questions for 12 13 and 14 plz
Answers: 2

Mathematics, 21.06.2019 20:00
If benito is selecting samples of five values from the table, which row will result in the greatest mean? population data row 1 4 2 2 3 3 row 2 3 3 4 3 2 row 3 2 4 3 4 3 row 4 3 4 4 7 3 row 1 row 2 r
Answers: 1
You know the right answer?
Breaking stuff let {xi} n i=1 be a sample of random variables of size n with the property that xi ∼...
Questions

Mathematics, 05.02.2021 14:00


Physics, 05.02.2021 14:00

Mathematics, 05.02.2021 14:00

Chemistry, 05.02.2021 14:00

Mathematics, 05.02.2021 14:00


English, 05.02.2021 14:00

History, 05.02.2021 14:00


Mathematics, 05.02.2021 14:00

Mathematics, 05.02.2021 14:00



Mathematics, 05.02.2021 14:00




Physics, 05.02.2021 14:00

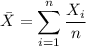
![\mathrm E[\bar X]=\displaystyle\frac1n\sum_{i=1}^n\mathrm E[X_i]=\frac{n\mu}n=\mu](/tpl/images/0082/8211/59b75.png)
![\mathrm V[\bar X]=\displaystyle\frac1{n^2}\mathrm V\left[\sum_{i=1}^nX_i\right]](/tpl/images/0082/8211/9cb21.png)
![\mathrm V[\bar X]=\displaystyle\frac1{n^2}\left(\sum_{i=1}^n\mathrm V[X_i]+2\sum_{1\le i](/tpl/images/0082/8211/4c8c7.png)
![\mathrm V[\bar X]=\displaystyle\frac1{n^2}\left(n\sigma^2+2\frac{n(n-1)}2\rho\sigma\right)](/tpl/images/0082/8211/de472.png)
![\mathrm V[\bar X]=\dfrac{\sigma^2}n+\dfrac{n-1}n\rho\sigma](/tpl/images/0082/8211/528fb.png)
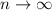 , we find that
, we find that ![\mathrm V[\bar X]\to\rho\sigma](/tpl/images/0082/8211/a1913.png) . Simply put, the failure of the CLT/LLN has to do with the fact that the
. Simply put, the failure of the CLT/LLN has to do with the fact that the 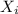 are not independent.
are not independent.

