The limit of (cos x + sin(2x) + 1)/(x^2 - pi^2) as x approaches pi is (a) 1/(2π) (b) 1/π (c) 1 (d) nonexistent

First, let's plug pi in for x to try to evaluate the limit:



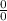This is equal to , however that does not necessarily mean that the limit is nonexistent. We can use L'Hospital's Rule by taking the derivative of both the numerator and denominator independently, then reevaluating the limit.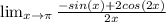



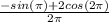
Plug pi in for  x again:



This is equal to  which simplifies to .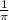

The answer is B.

Ithought this was