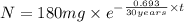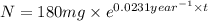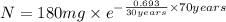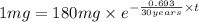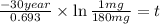Chemistry, 28.02.2020 19:22 gianababnnna
The half-life of cesium-137 is 30 years. Suppose we have a 180 mg sample. Find the mass that remains after t years. Let y(t) be the mass (in mg) remaining after t years. Then we know the following. y ( t ) = y ( 0 ) e k t = ⋅ e k t Since the half-life is 30 years, then y ( 30 ) = mg. Thus, e 30 k = . Therefore, k = . Now, remembering that ln x n = n ln x and that e ln z = z , we have y ( t ) = 180 e ( t / 30 ) ( − ln 2 ) = mg. How much of the sample remains after 70 years? After 70 years we have the following. y ( 70 ) = 180 ⋅ 2 = mg (Round your answer to two decimal places.) After how long will only 1 mg remain? To find the time at which only 1 mg remains, we must solve 1 = y ( t ) = 180 ( 2 − t / 30 ) , and so we get the following. t = − 30 log 2 ( ) Hence, we conclude the following. t = yr (Round your final answer to one decimal place.)

Answers: 2


Another question on Chemistry

Chemistry, 22.06.2019 05:50
What are transitions between a liquid and a solid called? identify which way they are transitioning
Answers: 2

Chemistry, 22.06.2019 11:40
Enzymes affect the reactions in living cells by changing the
Answers: 3

Chemistry, 22.06.2019 17:40
How much heat is added if 0.814g of water increase in temperature by 0.351 degree c?
Answers: 3

Chemistry, 22.06.2019 19:30
Estimate the molar mass of the gas that effuses at 1.6 times the effusion rate of carbon dioxide.
Answers: 1
You know the right answer?
The half-life of cesium-137 is 30 years. Suppose we have a 180 mg sample. Find the mass that remains...
Questions


Mathematics, 06.03.2021 01:00

History, 06.03.2021 01:00


Mathematics, 06.03.2021 01:00





Mathematics, 06.03.2021 01:00





Mathematics, 06.03.2021 01:00

Mathematics, 06.03.2021 01:00


Biology, 06.03.2021 01:00


History, 06.03.2021 01:00

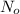 = 180 mg
= 180 mg

![t_{1/2}=30 years[p/tex]where, [tex]N_o](/tpl/images/0528/1653/35331.png) = initial mass of isotope
= initial mass of isotope
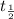 = half life of the isotope
= half life of the isotope
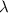 = rate constant
= rate constant