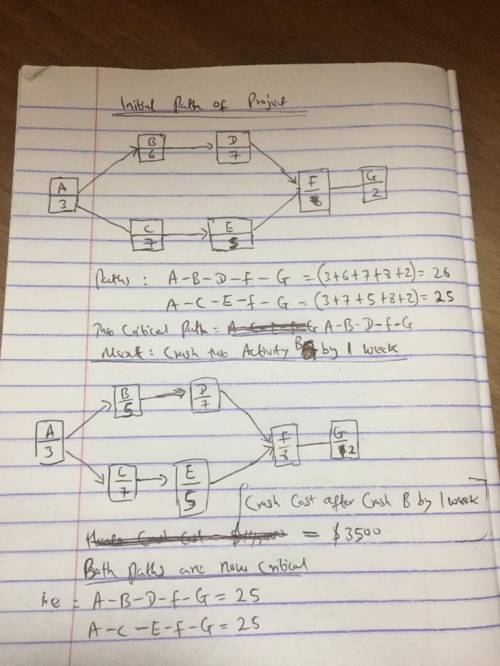
A project manager is faced with the following activities and times associated with a building construction for a cancer research facility. Each activity can be crashed at most by 2 weeks. The cost associated with each week time reduction is given below. (note: The 1st crash and 2nd crash costs are associated with the first and second time that a specific activity is crashed. So, if you crash Activity A once, the cost is $9,000, if you have to crash Activity A a second time, the cost is $9,500) Crash Costs
Activity Immediate Predecessor Normal Time (weeks) 1st crash 2nd crash

A 3 $9,000 $9,500
B A 6 $3,500 $6,000
C А 7 $4,000 $5,000
D B 7 $4,500 $6,000
E C 5 $7,000 $7,500
F D, E 8 $10,000 $12,000
G F 2 $14,000 $16,000

What is the minimum cost to crash this project by 2 weeks?

a. $12,000
b. $9,000
c. $16,000
d. $3,500

The monthly demand equation for an electric utility company is estimated to be p equals 60 minus left parenthesis 10 superscript negative 5 baseline right parenthesis x, where p is measured in dollars and x is measured in thousands of killowatt-hours. the utility has fixed costs of $3 comma 000 comma 000 per month and variable costs of $32 per 1000 kilowatt-hours of electricity generated, so the cost function is upper c left parenthesis x right parenthesis equals 3 times 10 superscript 6 baseline plus 32 x. (a) find the value of x and the corresponding price for 1000 kilowatt-hours that maximize the utility's profit. (b) suppose that the rising fuel costs increase the utility's variable costs from $32 to $38, so its new cost function is upper c 1 left parenthesis x right parenthesis equals 3 times 10 superscript 6 baseline plus 38 x. should the utility pass all this increase of $6 per thousand kilowatt-hours on to the consumers?